コンプリート！ 三 平方 の 定理 表 272485

 2平方定理 この定理はフェルマーの2平方定理とも呼ばれることがあり，証明はオイラーによってはじめてなされたとされています． 定理． 奇素数 (奇数かつ素数，すなわち 3 以上の素数) p p が 4 で割ると 1 余るとき， p p は 2 つの平方数の和として表さ三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角有名な 三 平方 の 定理 表 三角定規型 暗記しておくべき直角三角形があります それは三角定規の形です 三角定規は 2 種類あります その 2 種類は必ず暗記すべき特別な直角三角形です 45 45 90 まずはじめに直角二等辺三角形タイプです これは正方形半分タイプという名前で

正弦定理と余弦定理の公式の証明 理系ラボ

三 平方 の 定理 表

三 平方 の 定理 表- でした．これは三角錐でも四角錐でも，円錐でも使える公式です． この式に登場する \(\frac{1}{3}\)って何なの？という話をします． 三角形の面積と一緒？？ 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか？ ずばり，三角形 三平方の定理を利用して四角すい、円すいの体積を求める問題です。 まずは基本的な円錐、正四角錐の体積の求め方をしっかり確認してから、いろいろな応用問題を解くようにしてください。 円錐の体積 下のような底面積の半径が6cm、 17年2月14日

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

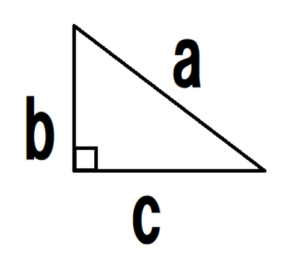
Made with Perfect Video http//googl/iacPmP三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。平方根 有理数と無理数 1 次の(あ)～(お)にあてはまる言葉を、①～⑤の中から選びなさい。 数 正の整数（ ） 0 2 次の①～⑤の中で、無理数であるものを選びなさい。 324 ① 自然数 ② 有理数 ③ 分数 ④ 無理数 ⑤ 負の整数

三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と3、4、5など3平方の定理との互換性があわない。 10 0645 60歳以上 / 会社員・公務員 / 非常に役に立った / 使用目的三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し

 これらの形を暗記すると、よりスピーディに計算できるようになります。 もちろん、万が一それぞれの辺の比を忘れてしまっても、直角三角形の \(2\) 辺の長さがわかっていれば、もう \(1\) 辺の長さは三平方の定理で導き出せるので、あわてないでくださいね。三平方の定理の逆 → 携帯版は別頁 《解説》 次のような直角三角形の三辺の長さについては， a 2b 2=c 2 が成り立ちます．（これを三平方の定理といいます．） 逆に，三辺の長さについて， a 2b 2=c 2 が成り立つとき，その三角形は直角三角形です自然数 が三個の平方数の和で表されるための必要十分条件は、,, {,,,,} により、 = () と表されることである。 逆に、 = () で表される自然数は三個の平方数の和で表されない。 これはディオファントスの時代から研究されてきた ことであるが、1798年、ルジャンドルによって証明された。

三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

かずお式中学数学ノート14 中3 円の性質・三平方の定理 著者の高橋一雄先生が「かずお式中学数学ノート14」（朝日学生新聞社刊）をテキストにして、ビデオ講義をしています。 内容は式の計算を扱っています。 テキストさえ購入していただければ、何度 三平方の定理を使って面積を求める方法は？ 問題を使って解説するよ！ 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に 有名な 三 平方 の 定理 表下記カテゴリー内の "三 平方 の 定理 空間 図形"に関連する他の関連記事を探す #三 平方 の 定理 空間 図形75三 平方 の 定理 は ピタゴラス ピタゴラスの定理 Wikipedia 印刷可能無料 三平方の定理 問題 難問 Fuutou Sozai

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

三平方の定理の応用 → 携帯版は別頁 三平方の定理 右図のような直角三角形については b2c2=a2 が成り立つ． 三平方の定理を使えば，直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる． たとえば右図では， b , c が分かっていれば a三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

三平方の定理 Geogebra

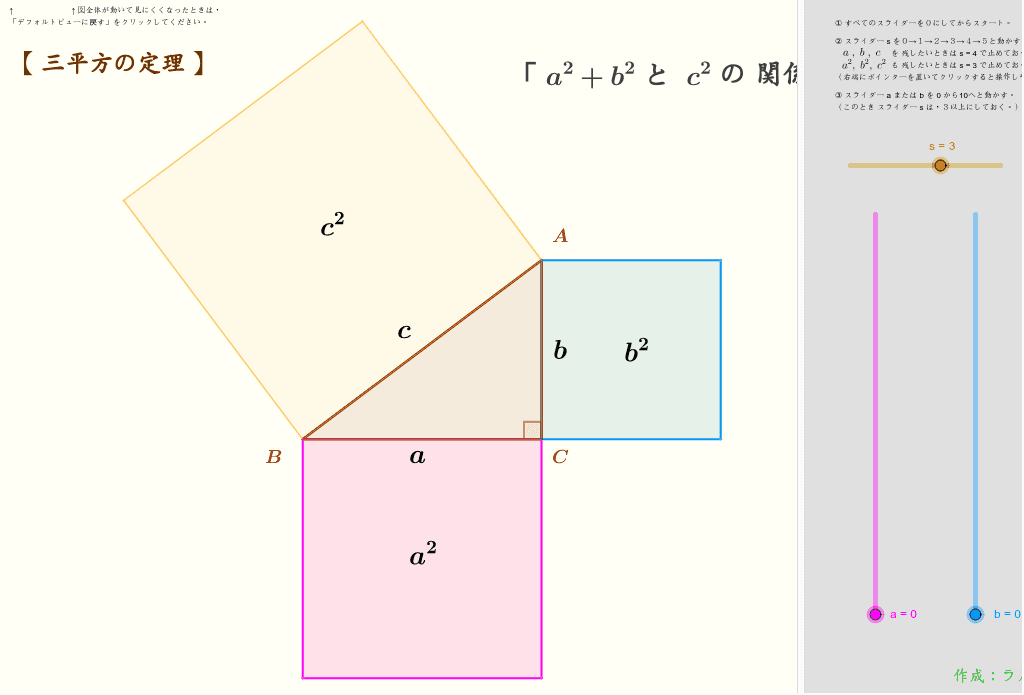
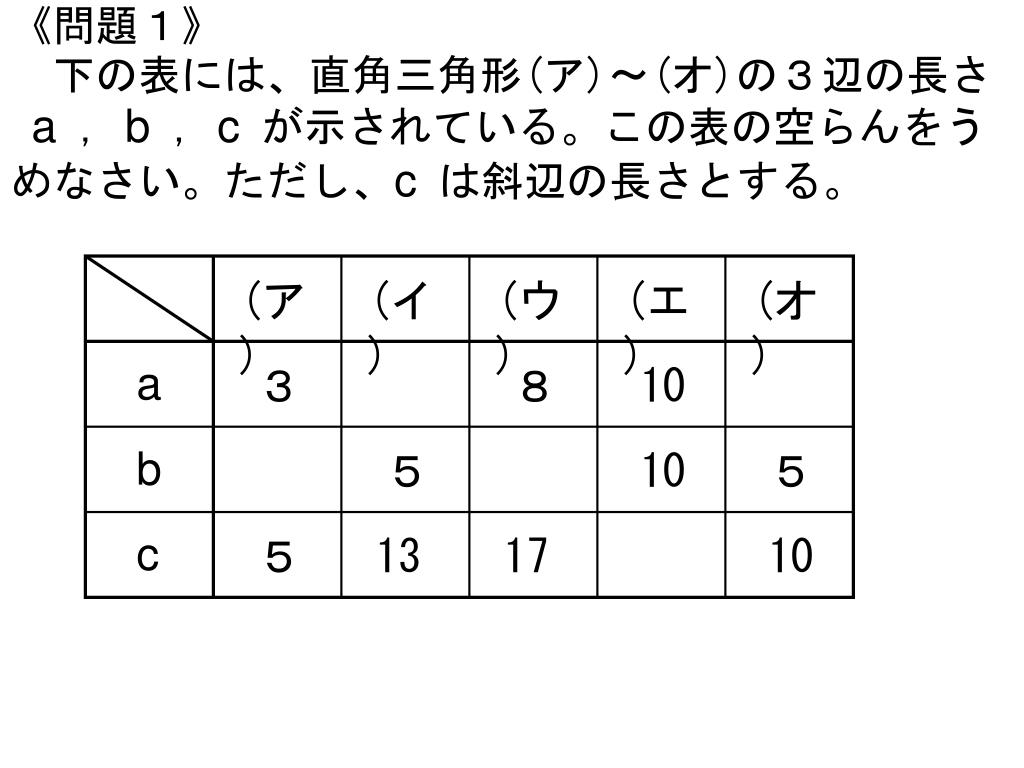
 つまり、下図のようになるよ！ ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこう！About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creatorsを1辺とする正方形の面積の値の関係を基に三 平方の定理を見いだし、それを証明することが できる。ワークシート記述の観察、発問に対す る生徒の発言の観察 第2時 三平方の定理を 利用する。 三平方の定理を利用して辺 の長さを求めること

三平方の定理から四立方の定理へ 東京図書出版

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

 三平方の定理には数百もの証明方法があります。今回は相似を利用した2つ目の証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理（ピタゴラスの定理） 上のような直角三角形で、次の等式が成り立つ。が成り立ちます。これで、三平方の定理を証明することができました！「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。三平方の定理（ピタゴラスの定理）と公式の証明忍者が用いた三角の知恵 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが 3 c m と 4 c m の直角三角形

三平方の定理 がひと目で分かる展示が面白いと話題に 視覚的にわかる こういうのが学校にあったら ねとらぼ

三角比 高校物理の備忘録

円錐の体積比を解説！ 円周角の定理 円周角の定理 必須の問題10選を解説！ 円周角の発展問題、円の中にブーメラン型！ 三平方の定理 初めに覚えておきたい三平方の基本公式！ 三平方の定理の逆ってなに？どうやって証明するの？1 代数学について 代数学は,「方程式を解く」ことを動機として形成され, 発展してきた 中学, 高校時代に学習した,「消去法 で連立1 次方程式を解く」, 「平方完成を用いて2 次方程式の根の公式を求める」というのは, 代数学におけ る最も根本的な考え方である この講義では, 現在の代数学の 新しい 三 平方 の 定理 応用 問題 数学 高校入試 無料学習プリント教材 Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor 中3数学 三平方の定理の応用 折り曲げ 2 Youtube平方根 平方根 平方根 (発展) 折り返し 三平方の定理と円 例題と練習 三平方の定理応用(面積) 三平方応用(体積表面積) 1年

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

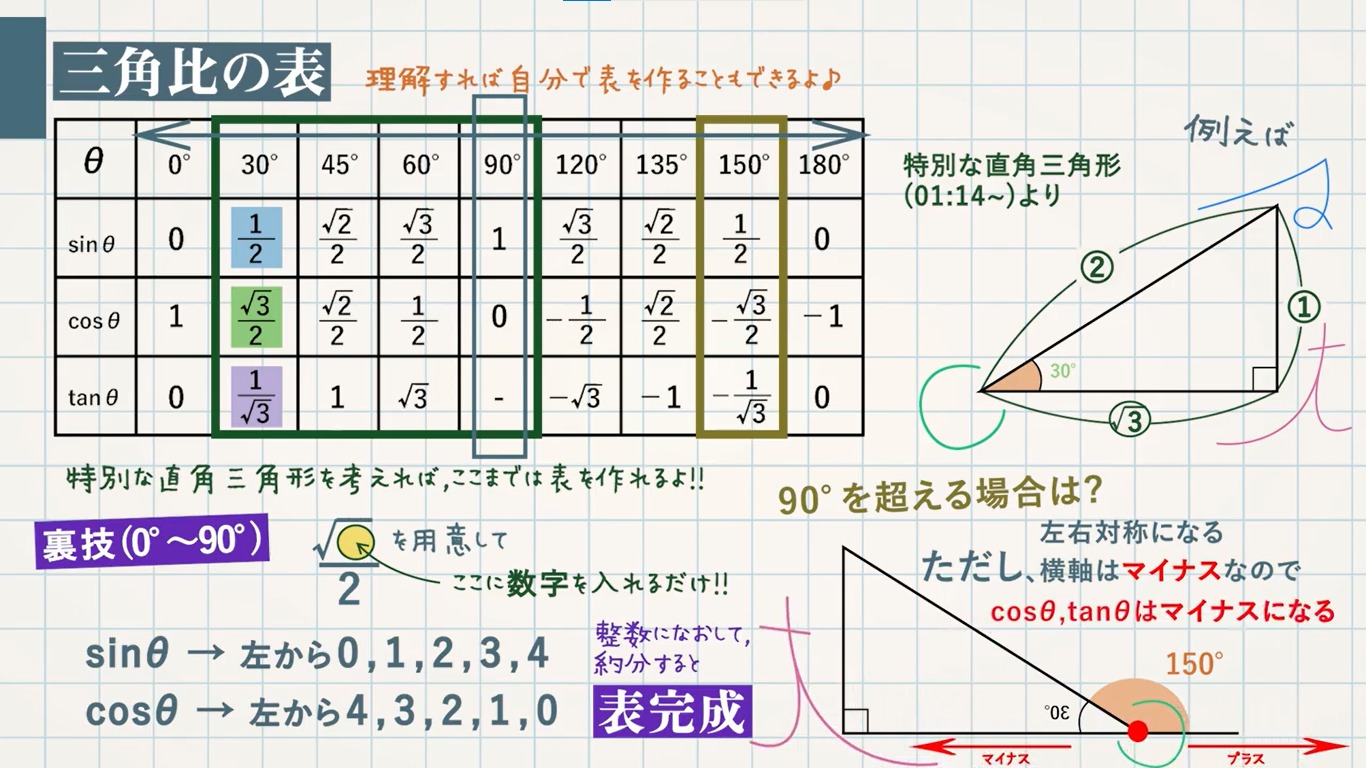
三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

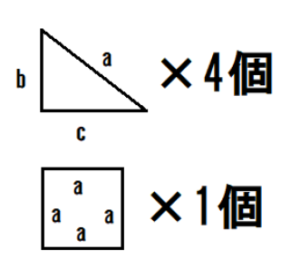
三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会

三平方の定理で辺を求める Youtube

1

Ppt ６ 三平方の定理 Powerpoint Presentation Free Download Id

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

1

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 覚えておきたい基本公式を解説 数スタ

三平方の定理 もう一度やり直しの算数 数学

三角比を考え方から理解する 有名角の三角比も説明

ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

三角比 高校物理の備忘録

数学 中3 61 三平方の定理 基本編 Youtube

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

三平方の定理 相似を利用した問題 問11の 2 を教えてください Clearnote

三平方の定理

わかりやすい三角比と基本公式 Irohabook

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学

3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist

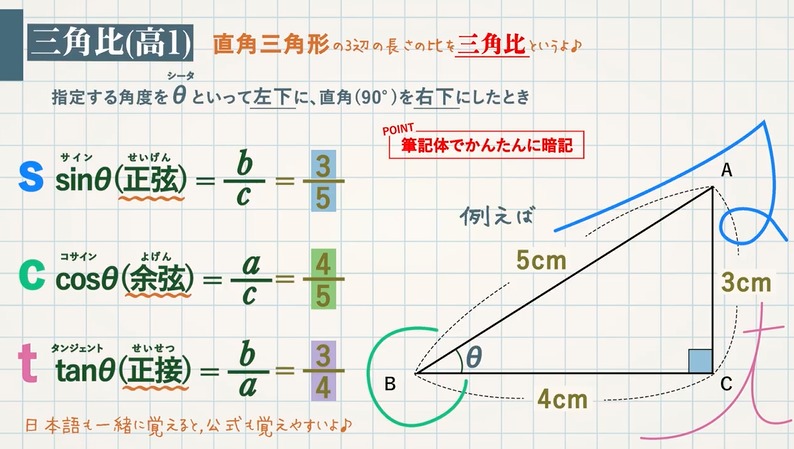
三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室

中3数学 三平方の定理の応用 75度に要注意 Youtube

７章 三平方の定理 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説

3

特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座

無料ダウンロード 三 平方 の 定理 表 シモネタ

三角関数とは コトバンク

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

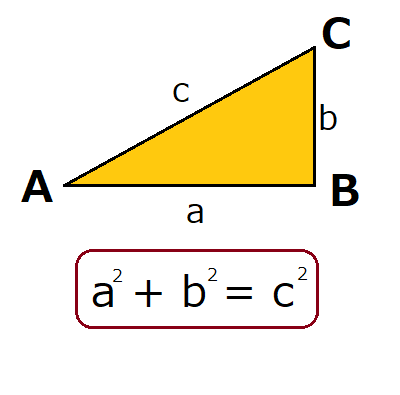
三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋all Rights Reserved

正弦定理と余弦定理の公式の証明 理系ラボ

1

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook

Oicsvvaua3ywvm

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

高校数学 三平方の定理による三角関数の計算 １ 映像授業のtry It トライイット

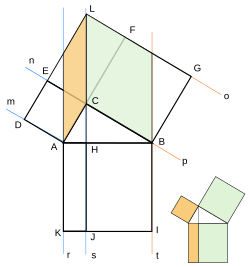
ピタゴラスの定理 Wikipedia

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

都立入試数学 三平方の定理を使わなくても解けるか 都立に入る

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理を教えてください Clearnote

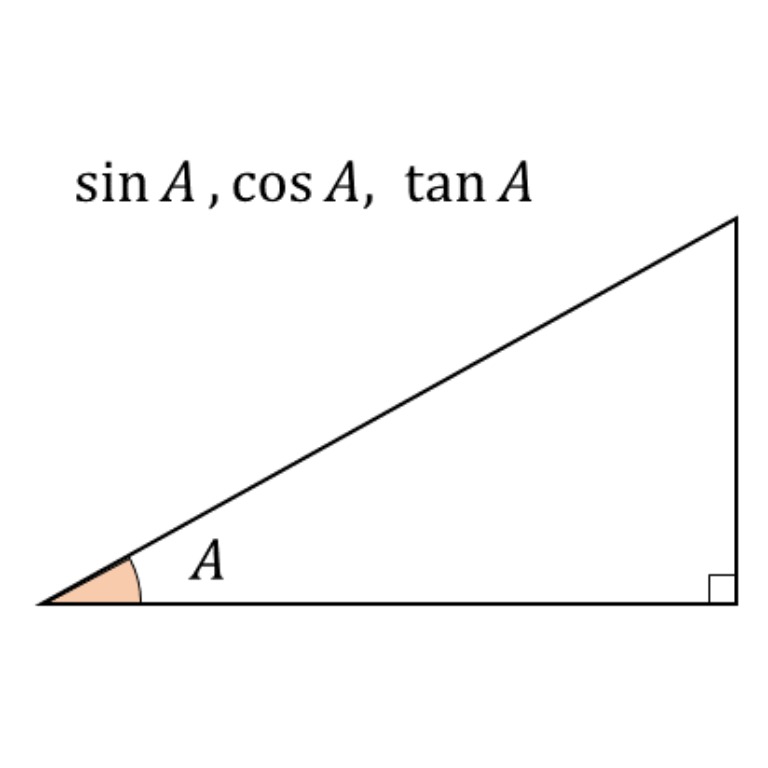
Tossランド 三角比 のコンテンツ集

答えはルート3です教えてください Clearnote

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

三平方の定理の４通りの美しい証明 高校数学の美しい物語

わかりやすい三角比と基本公式 Irohabook

三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

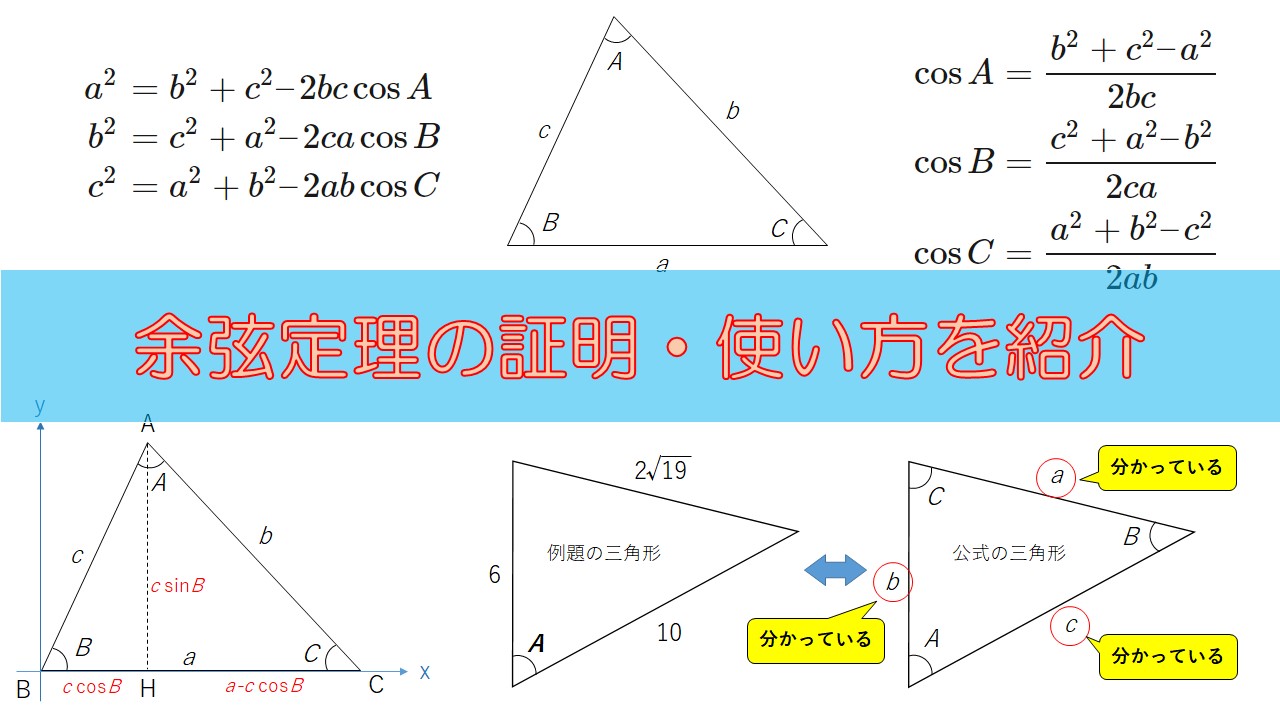
高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

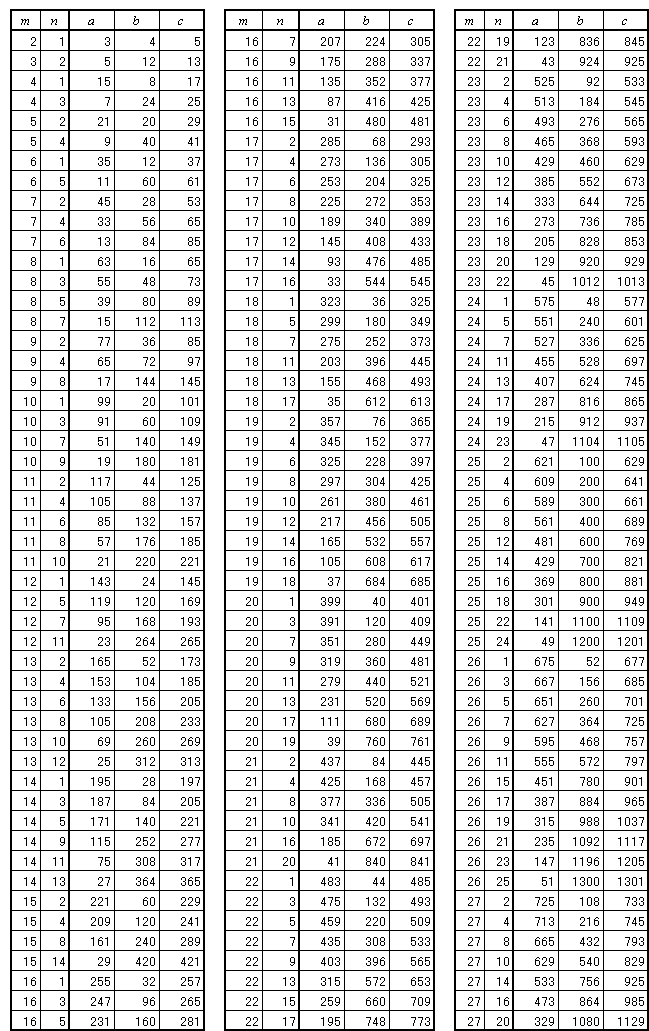
書評 ピタゴラスの定理

この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋

余弦定理の覚え方 語呂合わせやイメージで暗記しよう 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三平方の定理の４通りの美しい証明 高校数学の美しい物語

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

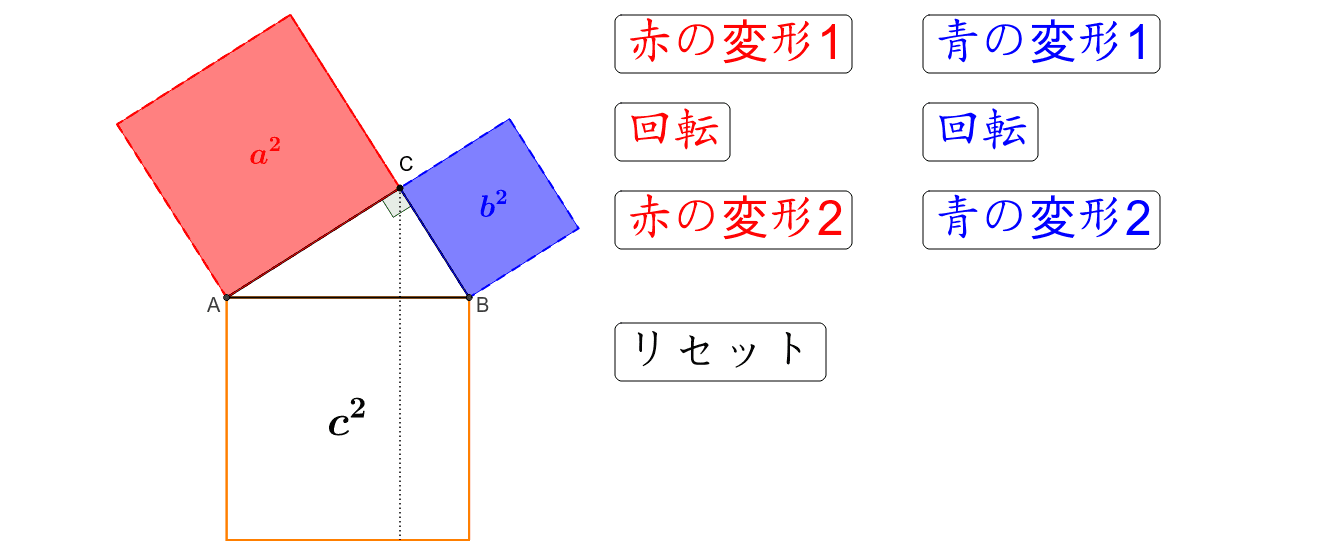
三平方の定理 Geogebra

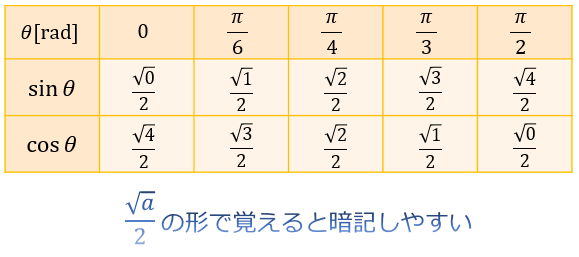
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

三平方の定理 覚えておきたい基本公式を解説 数スタ

三平方の定理とsin 2 Cos 2 1の違い たとえば次のような問題 Sina 2 数学 教えて Goo

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

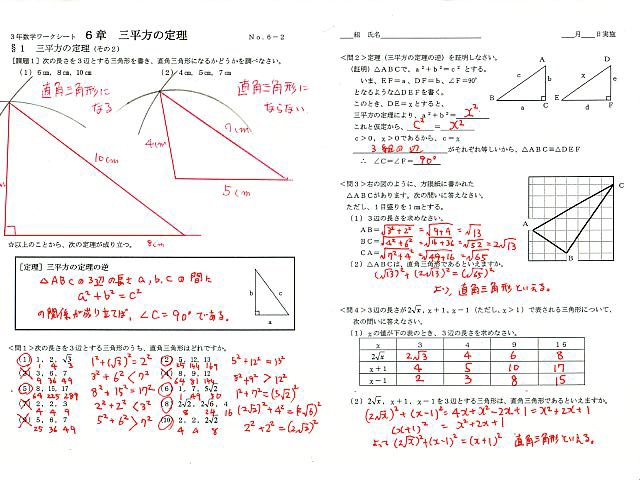
２ 三平方の定理の逆 Mathweather4067のblog

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理 自動計算サイト

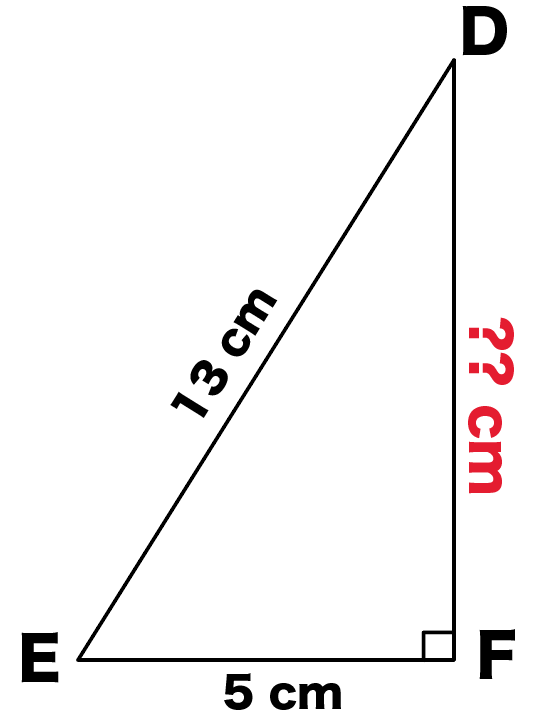
3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

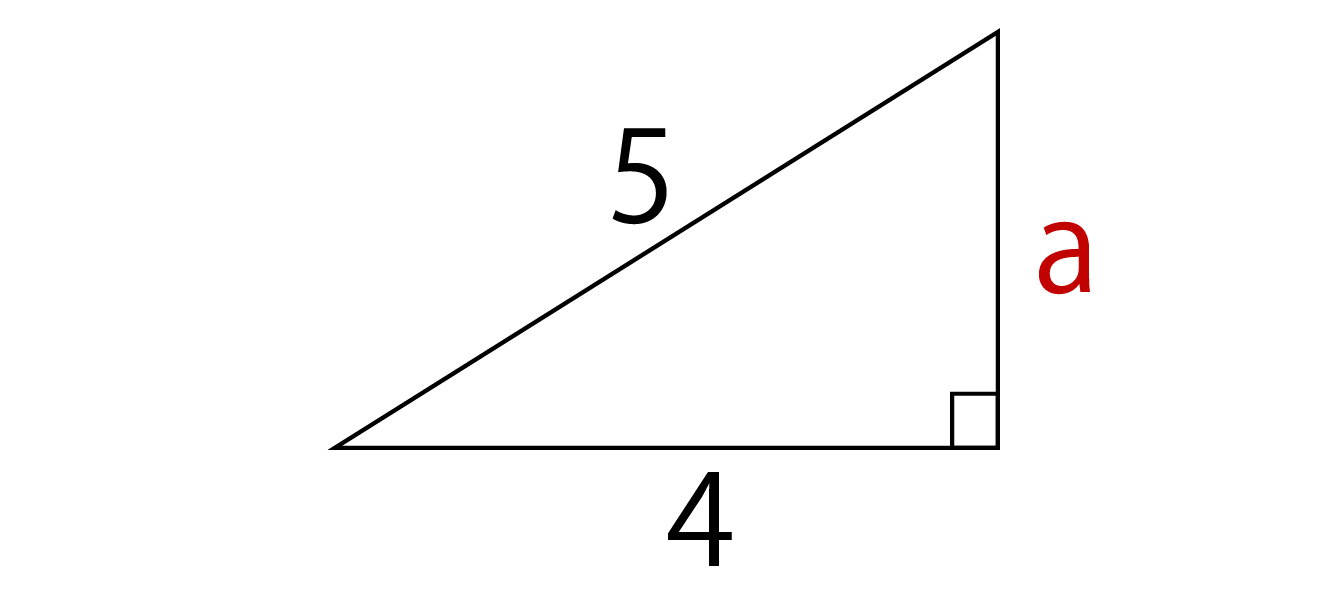
三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 覚えておきたい基本公式を解説 数スタ

Oicsvvaua3ywvm

名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

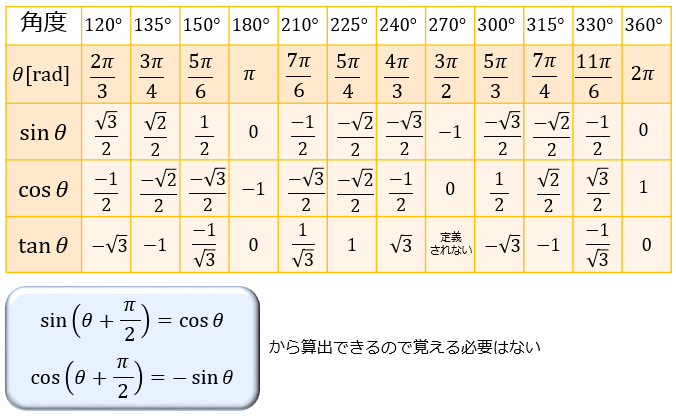
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

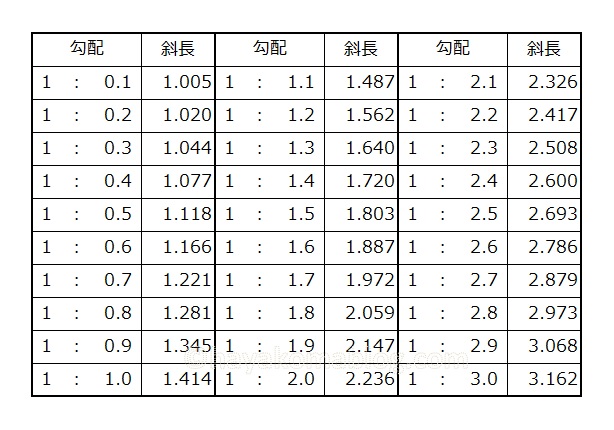
勾配 斜長 法長 斜辺 換算表

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

単位円とは 1分でわかる意味 覚え方 表 Sin Tanとの関係

無料 中３数学 基本解説 問題プリント 336 三平方の定理４ 空間図形